PINE LIBRARY
已更新 FunctionBlackScholes
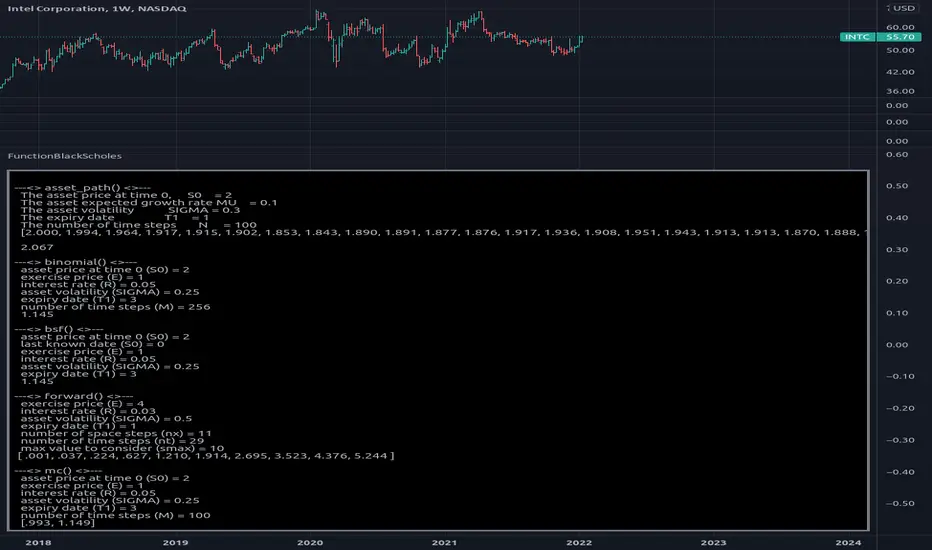
Library "FunctionBlackScholes"
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
發行說明
v2 fixed some issues.Pine腳本庫
秉持TradingView一貫精神，作者已將此Pine代碼以開源函式庫形式發佈，方便我們社群中的其他Pine程式設計師重複使用。向作者致敬！您可以在私人專案或其他開源發表中使用此函式庫，但在公開發表中重用此代碼須遵守社群規範。
免責聲明
這些資訊和出版物並非旨在提供，也不構成TradingView提供或認可的任何形式的財務、投資、交易或其他類型的建議或推薦。請閱讀使用條款以了解更多資訊。
Pine腳本庫
秉持TradingView一貫精神，作者已將此Pine代碼以開源函式庫形式發佈，方便我們社群中的其他Pine程式設計師重複使用。向作者致敬！您可以在私人專案或其他開源發表中使用此函式庫，但在公開發表中重用此代碼須遵守社群規範。
免責聲明
這些資訊和出版物並非旨在提供，也不構成TradingView提供或認可的任何形式的財務、投資、交易或其他類型的建議或推薦。請閱讀使用條款以了解更多資訊。