固定範圍成交量分佈圖
定義
固定範圍成交量分佈圖(FRVP)指標計算指定時間段內的成交量數據,允許交易者分析特定範圍的成交量活動,而不是資產的整個價格變動。
注意:您可以在成交量分佈圖指標:基本概念幫助中心文章中,閱讀有關所有成交量分佈圖指標共享特徵的更多資訊。下面的內容描述了該特定成交量分佈圖指標的獨特功能。如何將FRVP應用於您的圖表
1. 從圖表左側面板的繪圖工具列表中,選擇固定範圍成交量分佈圖,如下所示。
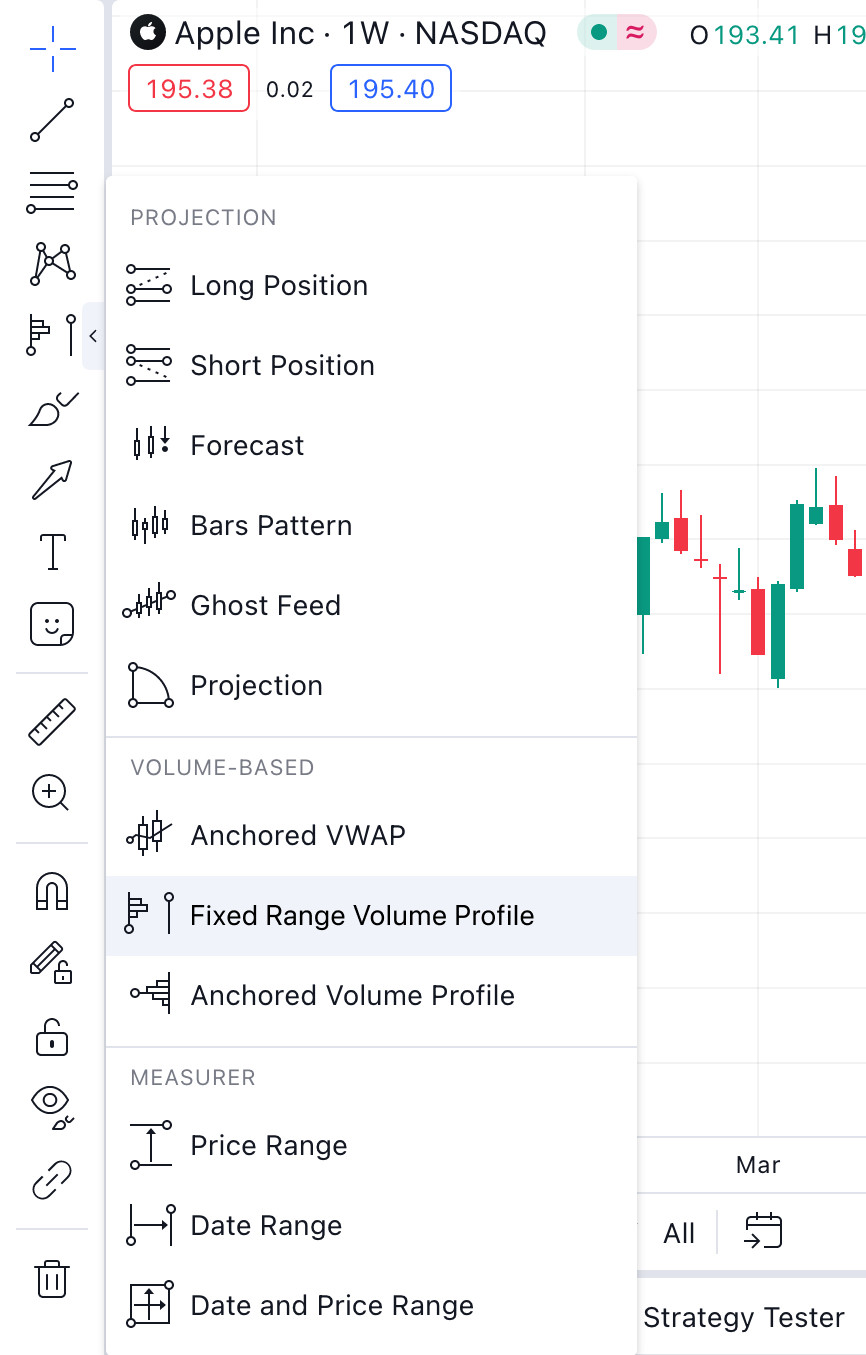
2. 點擊圖表以選擇您要開始計算的第一個點。

3. 點擊圖表上的另一個位置以選擇您要完成計算的第二個點。成交量分佈圖將顯示在圖表上,如下圖所示。

計算
在計算固定成交量分佈圖時,我們會依序檢查一系列時間週期,直到計算VP的時間週期內的長條圖數量少於5000條為止。時間週期的順序是:1分鐘、5分鐘、15分鐘、30分鐘、60分鐘、240分鐘、1天。如果指標涵蓋的K線圖總數為5分鐘或更少,或在任何以秒為基礎的時間週期上使用,則指標將從1 秒時間週期中獲取數據進行計算,而不管覆蓋的條形圖數量如何。
注意:在期貨和價差圖表上,成交量概況不是透過要求少於5000根K線的時間週期來計算的,而是根據上面的時間週期清單使用比當前時間範圍低一級的時間範圍。例外是所有基於秒的時間範圍,它們始終使用1S數據。考慮以下範例。FRVP指標被設定為:計算從每週的第一個星期一到最後一個星期日之間時段的分佈。該商品全天交易(為了進行實驗,我們假設不存在沒有交易發生的跳空,並且每週的每一分鐘都有一個與之關聯的K線)。
- 首先,指標檢查“1”時間週期,發現該商品的1m圖表具有7D * 1440m = 10080條1m數據,高於5000條限制。它選擇序列中的下一個時間週期。
- 接下來,指標對“3”時間週期執行相同的操作。該商品的3m圖表有7D * (1440 / 3) = 3360條數據。這低於5000條數據限制,因此FRVP計算中將使用3m週期。
注意:可用於指標計算的較低時間週期K線數量有限。如果FRVP設定在商品歷史記錄中非常深入地進行計算,則該時間段內可能沒有更低的時間週期資訊。在這種情況下,將使用圖表時間週期進行計算。
為了證明這一點,嘗試將FRVP增加到NASDAQ:AAPL, 1D,並將其設定從1980年12月12日開始的一天時間段。此時間週期不會有更低的時間週期數據,因此FRVP計算將以圖表週期(1D)進行。
建立在單根K線上
請注意,在單根K線上建構固定範圍成交量分佈圖時,收盤 > 開盤條件用於計算上漲/下跌成交量。即:如果收盤價 > 開盤價,則價格變動被視為上漲成交量,如果收盤價 <= 開盤價,則價格變動被視為下跌成交量。
輸入
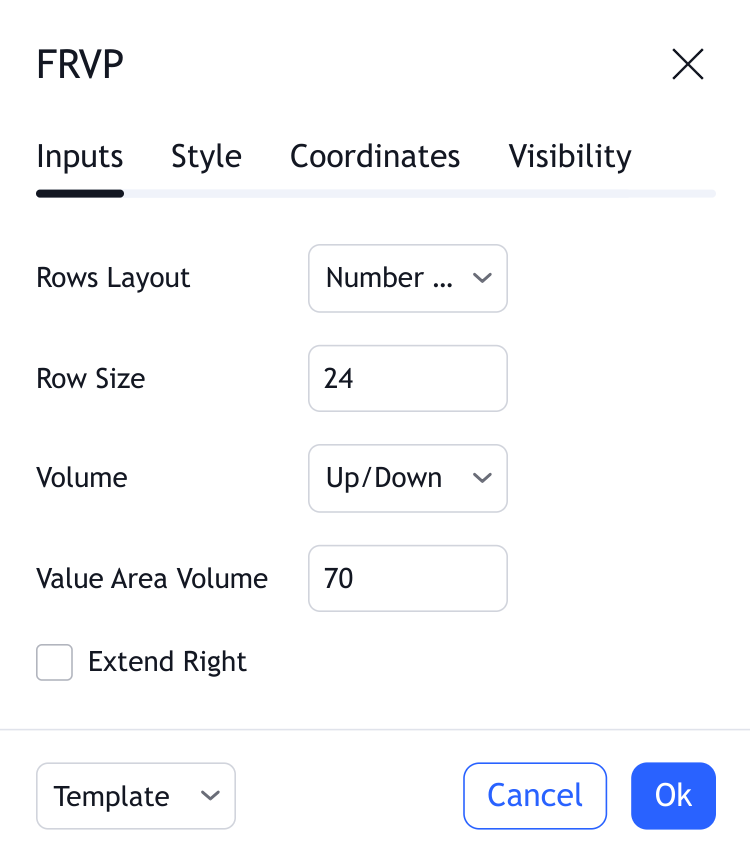
行版面/行大小
這兩個輸入指定指標計算每個K線圖將有多少行。
如果“行版面”設定為“行數”,則“行大小”輸入指定K線圖中的總行數,且每行的tick數是根據以下公式自動計算的:每行tick數= (K線圖頂部- K線圖底部) / 行數 / tick大小。根據K線圖的跨度,每行tick數的值可能會向上或向下四捨五入,且總行數可能會超過指定的限制。
讓我們考慮一個tick大小為0.01的商品,以及一個價格變動從10到11的成交量分佈圖K線圖,這使得它跨越的總tick數為100。如果「行大小」設定為25,則單行的高度為(3 - 2) / 25 / 0.01 = 4個tick。產生的K線圖有25行,每行跨越4個tick。
若行高度計算結果是浮點數,指標會對每行tick數的計算進行四捨五入,以確保高度為整數。它還可能會建立額外的行,以確保所有數據都在長條圖中得到表示。每行tick數的四捨五入取決於哪種方式使總行數更接近「行大小」輸入中的值。
例如:如果上述情況下「行大小」變更為30,則初始行高度為(3 - 2) / 30 / 0.01 = 每行3.333個tick。
如果這個數字被四捨五入到最接近的整數3,那麼生成的K線圖中的每行將有3個tick。因此,前30行只涵蓋了30 * 3 = 90個tick,而K線圖總共跨越了100個tick。這留下了10個tick沒有被涵蓋,因此額外創建了四行,前三行的大小為3,最後一行的大小為1,總行數增加到34。
若將其向上四捨五入,則K線圖中的每行高度為4個tick。在這種情況下,所有100個tick都適合在25行中,沒有剩餘。由於34行更接近30行,即請求的“行大小”,因此指標使用3個tick作為行高度。
如果設定為“每行tick數”,則行大小表示每行中的tick數(1個tick是此商品價格可以移動的最小單位。例如:對於NASDAQ,1個tick是0.01,因為價格需要至少移動0.01美元,也就是1美分)。例如:將其設為25,代表每行的高度為25個tick。在這種情況下,行數將自動計算,對於價格範圍從200到300的商品(tick大小為0.01),成交量分佈圖K線圖將有(300 - 200) / 0.01 / 25 = 400行。