Polynomial Regression Bands w/ Extrapolation of Price [Loxx]

2022年8月14日

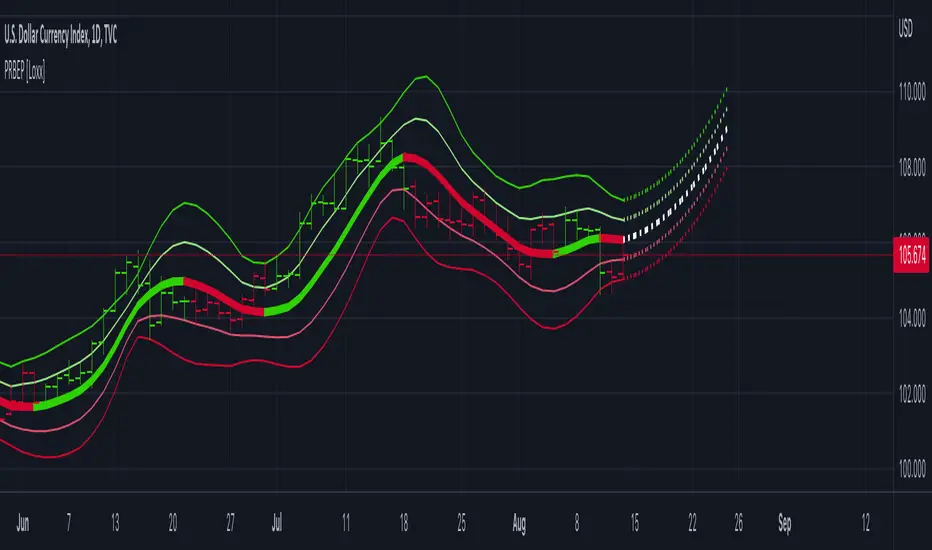
Polynomial Regression Bands w/ Extrapolation of Price [Loxx] is a moving average built on Polynomial Regression. This indicator paints both a non-repainting moving average and also a projection forecast based on the Polynomial Regression. I've included 33 source types and 38 moving average types to smooth the price input before it's run through the Polynomial Regression algorithm. This indicator only paints X many bars back so as to increase on screen calculation speed. Make sure to read the tooltips to answer any questions you have.

What is Polynomial Regression?
In statistics, polynomial regression is a form of regression analysis in which the relationship between the independent variable x and the dependent variable y is modeled as an nth degree polynomial in x. Polynomial regression fits a nonlinear relationship between the value of x and the corresponding conditional mean of y, denoted E(y |x). Although polynomial regression fits a nonlinear model to the data, as a statistical estimation problem it is linear, in the sense that the regression function E(y | x) is linear in the unknown parameters that are estimated from the data. For this reason, polynomial regression is considered to be a special case of multiple linear regression .

Related indicators
Polynomial-Regression-Fitted Oscillator [Loxx]

Polynomial-Regression-Fitted RSI [Loxx]

PA-Adaptive Polynomial Regression Fitted Moving Average [Loxx]

Poly Cycle [Loxx]

Fourier Extrapolator of Price w/ Projection Forecast [Loxx]