OPEN-SOURCE SCRIPT
Automated Option Price - Black-Scholes model
Please make sure you are plotting this indicator on DAILY bars, not doing so will lead to unintended results. Also, make sure that you keep up to date the Risk-free interest rate, which you can consult (for U.S.) on ycharts.com.
This is an indicator that is meant to be used for Options Day Trading, but it can be useful for mid-term or leaps for I also enabled the possibility for user to input manually the Strike and Expiration date. I based the calculation on the Black-Scholes model. Variables included in the calculation are:
-Stock price (S): The current price of the underlying asset (e.g., a stock).
-Strike price (K): The predetermined price at which the option can be exercised.
-Time to expiration (T): The time remaining until the option expires, expressed as a fraction of a year.
-Volatility (σ): The annualized standard deviation of the stock's returns, which is a measure of the stock's price fluctuations.
-Risk-free interest rate (r): The annualized return on a risk-free investment, often approximated by the yield on a government bond.
The only variable I excluded from the original model was the Dividend yield (q).
U S E R I N P U T S:
1. AUTOMATIC calculations enabled:
i) Strike price (K):
Automatically calculate the strike price for both call and put options based on the stock's closing price. The logic follows a set of rules to determine the strike prices which will usually be Out-of-the-Money (OTM):
-If the stock's closing price is between 1 and 60, the call strike price is rounded up to the nearest whole number, while the put strike price is rounded down to the nearest whole number.
-If the stock's closing price is between 60 and 90, the call strike price is rounded up to the nearest whole number and increased by 1, while the put strike price is rounded down to the nearest whole number and decreased by 1.
-If the stock's closing price is between 90 and 120, the call strike price is rounded up to the nearest whole number and increased by 2, while the put strike price is rounded down to the nearest whole number and decreased by 2.
-If the stock's closing price is above 120, the call strike price is rounded up to the nearest multiple of 5, while the put strike price is rounded down to the nearest multiple of 5.
By applying these rules, I just tried to ensure that the automatically calculated strike prices are tailored to the stock's price range, allowing for more accurate option pricing calculations.
ii) Time to expiration (T):
The indicator will consider this week’s expiration contracts (Friday) only when the current day/bar = Monday. If Tuesday or older it will consider the expiration date of the next week’s Friday (because we are not Theta gamblers, right?).
If you are not comfortable with above for whatever reason, you can always…
2. Enter inputs MANUALLY
First make sure you UNTICK the boxes for automatic calculation.
i) Strike price (K) – Self-explanatory
ii) Time to expiration (T) – Just make sure that the horizon you are inputting matches with the next parameter (e.g. you would not input a Monthly risk-free interest rate for a Leap).
iii) Risk-free interest rate (r) – You can pull this data from the web. Here’s the link I used to define the value that this indicator was launched with:
ycharts.com/
Don’t get obsessed with updating this daily if you are using this for day trading, you will notice that weekly may be more than enough.
V O L A T I L I T Y
Not option to manually input Volatility so I’ll explain how it is calculated in this script:
I considered two measures of volatility; one is derived calculating the annualized volatility using the standard deviation of daily returns and the second one is the ATR-based annualized volatility. I then used a ‘combined’ approach with the harmonic mean and the arithmetic mean of these results which can help account for the variability in the option prices calculated with different volatility estimates, which can be more robust when dealing with outliers or skewed data. I back tested with some samples of actual option prices and found that this approach is the one that got results closer to the actual bids.
T A B L E
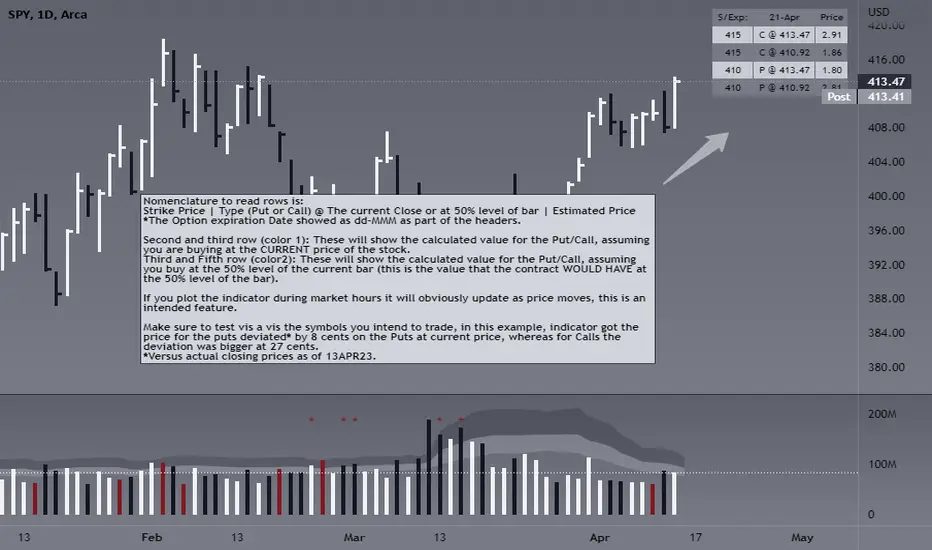
Nomenclature to read rows is:
Option Strike Price | Type of Option (Put or Call) @ The current Close or at 50% level of bar | Estimated Price
*The Option expiration Date showed as dd-MMM as part of the headers.
Second and third row (color 1): These will show the calculated value for the Put/Call, assuming you are buying at the CURRENT price of the stock.
Third and Fifth row (color2): These will show the calculated value for the Put/Call, assuming you buy at the 50% level of the current bar (this is the value that the contract WOULD HAVE at the 50% level of the bar).
If you plot the indicator during market hours it will obviously update as price moves, this is an intended feature.
L I M I T A T I O N S
The Black-Scholes model, like many other models, has its limitations and will oftentimes provide inaccurate option prices in all market conditions. High volatility events, such as earnings announcements, can lead to significant price fluctuations that are not fully captured by the model.
The model assumes that the stock price follows a continuous random walk with constant volatility, but in reality, volatility can change over time, and stock prices can exhibit jumps, especially around significant events like earnings announcements. This can cause the model to underestimate the true option price in such situations.
Please make sure that you first back test on the symbols you trade to ensure the information presented by this indicator will suit your trading strategy. You will find that the delta between the proposed price of the indicator versus the actual price may differ significantly in some symbols while for others it will be very close. For instance, today (13APR23), the prices for AMD, DIS, AAPL (puts only), were very close to actual bids, whereas TSLA differ significantly (but then again, take a look at the calendar and this last symbol is having earnings next week which may add a premium to the contracts)… I am sure you will get your own conclusions and applicable use cases based on the data you test with.
As always, be wise and methodical on the investment or trading decisions you make!
This is an indicator that is meant to be used for Options Day Trading, but it can be useful for mid-term or leaps for I also enabled the possibility for user to input manually the Strike and Expiration date. I based the calculation on the Black-Scholes model. Variables included in the calculation are:
-Stock price (S): The current price of the underlying asset (e.g., a stock).
-Strike price (K): The predetermined price at which the option can be exercised.
-Time to expiration (T): The time remaining until the option expires, expressed as a fraction of a year.
-Volatility (σ): The annualized standard deviation of the stock's returns, which is a measure of the stock's price fluctuations.
-Risk-free interest rate (r): The annualized return on a risk-free investment, often approximated by the yield on a government bond.
The only variable I excluded from the original model was the Dividend yield (q).
U S E R I N P U T S:
1. AUTOMATIC calculations enabled:
i) Strike price (K):
Automatically calculate the strike price for both call and put options based on the stock's closing price. The logic follows a set of rules to determine the strike prices which will usually be Out-of-the-Money (OTM):
-If the stock's closing price is between 1 and 60, the call strike price is rounded up to the nearest whole number, while the put strike price is rounded down to the nearest whole number.
-If the stock's closing price is between 60 and 90, the call strike price is rounded up to the nearest whole number and increased by 1, while the put strike price is rounded down to the nearest whole number and decreased by 1.
-If the stock's closing price is between 90 and 120, the call strike price is rounded up to the nearest whole number and increased by 2, while the put strike price is rounded down to the nearest whole number and decreased by 2.
-If the stock's closing price is above 120, the call strike price is rounded up to the nearest multiple of 5, while the put strike price is rounded down to the nearest multiple of 5.
By applying these rules, I just tried to ensure that the automatically calculated strike prices are tailored to the stock's price range, allowing for more accurate option pricing calculations.
ii) Time to expiration (T):
The indicator will consider this week’s expiration contracts (Friday) only when the current day/bar = Monday. If Tuesday or older it will consider the expiration date of the next week’s Friday (because we are not Theta gamblers, right?).
If you are not comfortable with above for whatever reason, you can always…
2. Enter inputs MANUALLY
First make sure you UNTICK the boxes for automatic calculation.
i) Strike price (K) – Self-explanatory
ii) Time to expiration (T) – Just make sure that the horizon you are inputting matches with the next parameter (e.g. you would not input a Monthly risk-free interest rate for a Leap).
iii) Risk-free interest rate (r) – You can pull this data from the web. Here’s the link I used to define the value that this indicator was launched with:
ycharts.com/
Don’t get obsessed with updating this daily if you are using this for day trading, you will notice that weekly may be more than enough.
V O L A T I L I T Y
Not option to manually input Volatility so I’ll explain how it is calculated in this script:
I considered two measures of volatility; one is derived calculating the annualized volatility using the standard deviation of daily returns and the second one is the ATR-based annualized volatility. I then used a ‘combined’ approach with the harmonic mean and the arithmetic mean of these results which can help account for the variability in the option prices calculated with different volatility estimates, which can be more robust when dealing with outliers or skewed data. I back tested with some samples of actual option prices and found that this approach is the one that got results closer to the actual bids.
T A B L E
Nomenclature to read rows is:
Option Strike Price | Type of Option (Put or Call) @ The current Close or at 50% level of bar | Estimated Price
*The Option expiration Date showed as dd-MMM as part of the headers.
Second and third row (color 1): These will show the calculated value for the Put/Call, assuming you are buying at the CURRENT price of the stock.
Third and Fifth row (color2): These will show the calculated value for the Put/Call, assuming you buy at the 50% level of the current bar (this is the value that the contract WOULD HAVE at the 50% level of the bar).
If you plot the indicator during market hours it will obviously update as price moves, this is an intended feature.
L I M I T A T I O N S
The Black-Scholes model, like many other models, has its limitations and will oftentimes provide inaccurate option prices in all market conditions. High volatility events, such as earnings announcements, can lead to significant price fluctuations that are not fully captured by the model.
The model assumes that the stock price follows a continuous random walk with constant volatility, but in reality, volatility can change over time, and stock prices can exhibit jumps, especially around significant events like earnings announcements. This can cause the model to underestimate the true option price in such situations.
Please make sure that you first back test on the symbols you trade to ensure the information presented by this indicator will suit your trading strategy. You will find that the delta between the proposed price of the indicator versus the actual price may differ significantly in some symbols while for others it will be very close. For instance, today (13APR23), the prices for AMD, DIS, AAPL (puts only), were very close to actual bids, whereas TSLA differ significantly (but then again, take a look at the calendar and this last symbol is having earnings next week which may add a premium to the contracts)… I am sure you will get your own conclusions and applicable use cases based on the data you test with.
As always, be wise and methodical on the investment or trading decisions you make!
開源腳本
在真正的TradingView精神中，這個腳本的作者以開源的方式發佈，這樣交易員可以理解和驗證它。請向作者致敬！您可以免費使用它，但在出版物中再次使用這段程式碼將受到網站規則的約束。 您可以收藏它以在圖表上使用。
免責聲明
這些資訊和出版物並不意味著也不構成TradingView提供或認可的金融、投資、交易或其他類型的意見或建議。請在使用條款閱讀更多資訊。