Euler Cubes - Cubᵋ

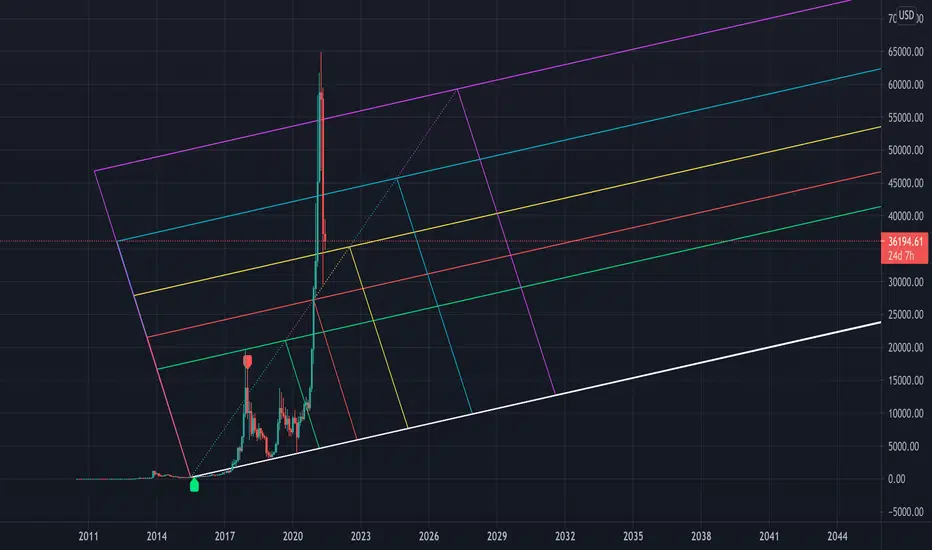
I give you the "Euler Cubes", inspired by the mathematical number 'e' (Euler's number).
It is suggested (fibonacci ratios analogy) that price/e ratio can give Support/Resistance area's.

The first cube is made by a low/high of choice, for example:

You set the 'source low'/'source high' in position:

Then you choose the 'e ratio' (x times 'e')
This multiplies the distance 'high-low' times '0.271828' times 'the set number'.
For example, choosing 5 gives 5x 0.271828 = 1.35914, the distance 'high-low' hereby multiplied by 1.35914, the following cubes multiply the previous distance by 1.35914.
(Settings below 5 will give cubes smaller than the 'high-low' distance)

In the case of x times 'e' = 5:

You can extend the lines:

Now you can give it an angle:

Do mind, using it over very little bars and using an angle can cause some lines to not align as intended, because for now, it is not possible to plot in between bars.

There are also 'Euler' SMA and EMA available with following length's:
27, 54, 82,109, 136, 163, 190 and 217

Cheers!

發行說明

When you want to choose a bar way back in history, you can enable
'Year - Month - Day', choose the date, and work from there further back

發行說明

Added constant's:
- Euler-Mascheroni constant gamma γ = 0.57721566490153286060651209008240243...
('Euler's constant', not to be confused with the constant e=2.718281...)
- golden ratio conjugate constant = 0.6180339887498948 = math.rphi
- the golden ratio constant = 1.6180339887498948 = math.phi
- Euler's number (Leonhard Euler) e = 2,71828182845904523536028747135266249... = math.e
- Archimedes' constant pi π = 3.1415926535897932 = math.pi
- constant of Mitchell Feigenbaum δ ≈ 4.66920160910299067185320382046620161...